WIS-je-dat?
Op deze pagina staan diverse PDF-bestanden met een kleine wiskundige
vraagstelling uitgewerkt. Het aantal sterren staat voor de
moeilijkheidsgraad van het onderwerp. De documenten zijn vrij te
gebruiken voor niet-commerciële onderwijsdoeleinden, mits de bron
vermeld wordt.
Een vader wil de code van zijn kluis aan zijn twee zoons geven. Maar
hij is bang dat de ene zoon de ander bedondert. Ze mogen de code alleen
kunnen gebruiken als ze samenwerken. Hoe kun je dat wiskundig voor
elkaar krijgen?
Stel dat je drie derdemachten bij elkaar optelt: \(k=a^3+b^3+c^3\) met
\(a\), \(b\) en \(c\) gehele getallen die ook negatief mogen zijn. Kun
je dan elk getal \(k\) maken? Heel lang was er geen oplossing voor
\(k=33\) en \(k=42\), maar nu...
Iedereen heeft geleerd hoe hij breuken moet optellen en vereenvoudigen.
En misschien ook wel hoe je met wortels om moet gaan. Sommige dingen
worden vaak fout gedaan. Maar is het antwoord dan ook altijd fout?
Een vierkant is plat en twee-dimensionaal. Een kubus is ruimtelijk en
drie-dimensionaal. Wat nu als we de reeks voortzetten? Vier-dimensionaal?
Een lastig probleem bij rijles. Maar hoe groot moet het gat tussen twee
auto's zijn om nog nét in één vloeiende beweging
achteruit in te kunnen parkeren?
\(38^2=1444\). Zijn er kwadraten die nog meer gelijke eindcijfers
hebben? En hoe zit dat met hogere machten?
Door gebruik te maken van een raaklijn aan de logaritmische functie, zie
je snel dat \(e^\pi>\pi^e\).
\(1/7=0,142857...\) Na deze zes cijfers herhaalt de breuk zich. Hoe zit
dat met het aantal repeterende cijfers in breuken? Het document bevat
een klein stukje C-code.
\(d=24\) is het grootste getal waarvoor de groep repeterende cijfers van
de breuk \(1/d\) in geen enkel talstelsel meer dan twee cijfers groot
is. Om dit te laten zien wordt gebruik gemaakt van de stelling van Euler
en de Carmichael-functie.
De cijfers op een digitale klok zijn redundant. De led-streepjes
herbergen meer informatie dan strikt noodzakelijk is. Ook bij een CD-rom
wordt gebruik gemaakt van redundante informatie. Het maakt de data
robuust.
De klassieke Pythagorasboom is goed bekend. Maar hoe erg lijkt deze op
een gewone boom, wanneer je deze uitbreidt naar drie dimensies? Het
document bevat code om dit zelf in
POV-ray te maken.
Met een eenvoudige spreadsheet maak je een fractale afbeelding. In het
document uitleg en screen shots.
In intelligentietests wordt vaak gevraagd wat het volgende getal in een
rijtje is. Maar hoe intelligent is die vraag eigenlijk? En wat zijn
logische antwoorden?
Stapel allemaal identieke stenen aan de rand van een tafel. Hoe ver kan
de bovenste steen maximaal over de tafelrand steken?
Een paar eeuwen voor Christus wist de Griek Archimedes al een
fantastische benadering te maken van \(\pi\). Hij deed dat door veelhoeken met
steeds meer zijdes in een cirkel te tekenen. Zo wist hij dat \(\pi\) tussen
\(3\frac{10}{71}\) en \(3\frac{1}{7}\) moest liggen.
Stel dat je een kubus zo hard in een mand gooit, dat deze dwars
door de bodem valt. Welke vorm kan het gat dan hebben?


 Gedeeld en toch geheim
Gedeeld en toch geheim Driemaal
tot de derde
Driemaal
tot de derde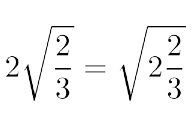 Echt fout!
Echt fout! 1,
2, 3, 4... kubus op papier
1,
2, 3, 4... kubus op papier Achteruit inparkeren
Achteruit inparkeren Eindcijfers
Eindcijfers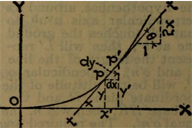 \(e^\pi>\pi^e\)
\(e^\pi>\pi^e\) In de herhaling
In de herhaling Klok kijken
Klok kijken Pythagorasboom
Pythagorasboom Tapijt van Sierpinski
Tapijt van Sierpinski Het volgende getal
Het volgende getal Stenen stapelen
Stenen stapelen Archimedes, Pythagoras en... \(\pi\)
Archimedes, Pythagoras en... \(\pi\) Door de mand gevallen
Door de mand gevallen